Seconda prova maturità 2025, da Cicerone a Cartesio: ecco i testi integrali di tutte le tracce - FOTO

Seconda prova maturità 2025,  tutte le tracce per i diversi indirizzi

Oggi 19 giugno inizia la seconda prova della Maturità 2025. Gli studenti affronteranno sfide diverse in base al proprio indirizzo. Per il liceo classico, ad esempio, c'è da tradurre una versione di latino di Cicerone tratta dal "De amicitia". Di seguito tutte le tracce della seconda prova divise per indirizzo: 

Liceo Classico (in gallery le pagine seguenti)

A001 – ESAME DI STATO CONCLUSIVO DEL SECONDO CICLO DI ISTRUZIONE
Indirizzi: LI01 – EA01 – CLASSICO

(Testo valevole anche per gli indirizzi quadriennali LI21, LIIC e LIQ1)
Disciplina: LINGUA E CULTURA LATINA

La vera natura dell’amicizia

Nel dialogo Laelius de amicitia, composto nel 44 a.C. ma ambientato nel 129 a.C., Cicerone descrive con accenti accorati l’amicizia tra due esponenti di primo piano della classe politica romana dell’epoca, Gaio Lelio e Scipione Emiliano, da poco scomparso. L’occasione è propizia per riflettere – Lelio che parla, ma in realtà Cicerone che si serve di questo vicenda, di questi personaggi – su un tema molto ampio e risulta essenziale per rinsaldare i legami che sono alla base della convivenza civile.

PRIMA PARTE: traduzione di un testo in lingua latina

PRE-TESTO

Saeplssime igitur mihi de amicitia cogitanti maxime illud considerandum videri solet, utrum propter imbecillitatem atque inopiam desiderata sit amicitia, ut dandis recipiendisque meritis, quod quisque minus per se ipse posset, id acciperet ab alio vicissimque redderet, an esset hoc quidem proprium amicitiae, sed antiquior et pulchrior et magis a natura ipsa profecta alia causa.

Molto spesso, quando rifletto sull’amicizia, mi sembra che si debba considerare prima d’ogni cosa questo: se l’amicizia sia desiderata per la debolezza nostra e la scarsità dei nostri mezzi, cosicché, dando e ricevendo favori, ciò che uno da sé non potesse fare, lo ricevesse da un altro e a sua volta lo contraccambiasse; o questo, sì, sia il proprio dell’amicizia, ma la causa ne sia un’altra, più intima e più bella e più veramente naturale.

TESTO

Amor enim, ex quo amicitia nominata est, princeps est ad benevolentiam coniungendam. Nam utilitates quidem etiam ab eis percipiuntur saepe, qui simulatione amicitiae coluntur et observantur temporis causa. In amicitia autem nihil fictum est, nihil simulatum est, et, quidquid est, id est verum et voluntarium. Quapropter a natura ipsa videtur profecta amicitia, cum intereos, qui se amant, et benevolentia et caritate iunguntur, ab eaque caritate, quamquam exspectatio fructus nulla subest, tamen amicitia delectat etiamsi nihil utilitatis ex ea proveniat. Quod si utilitas amicitias confirmaret, eadem commutatio utilitatum caritatem conciliaret non amicitias, quae, cum a caritate profecta sit, nec ab utilitate umquam potest dissolvi. Ex quo efficitur, ut et utilitatem amicitia, non utilitas amicitias pariat. Illud autem verum est, nec sine causa, quod a sapientibus dicitur, quod, qui ipsi sibi plurimum confidunt et virtute et sapientia sic armati sunt, ut nullius egere videantur, iis maxime opus esse amicitia sententiaeque eorum ad verum consilium cum amicorum tum etiam multitudinis usum pervenire. Quamquam hoc inter amicos, ut inter bonos, iucundum est, quod aeque uterque alteri studet, ut, quasi quaedam emulatio dignitatis exsistat, quamquam uno in loco sit amicitia. Itaque non aqua, non igne, ut aiunt, pluribus in locis utimur quam amicitia. Neque ego nunc de vulgari aut de mediocri, quae tamen ipsa et delectat et prodest, sed de vera et perfecta loquor, qualis eorum, qui pauci nominantur, fuit. Nam et secundas res splendidiores facit amicitia et adversas partiens communicansque leviores.

POST-TESTO

Quis est qui C. Fabrici, M. Curi non cum caritate aliqua et benevolentia memoriam usurpet, quos umquam vidit? Quis autem est qui Tarquinium Superbum, qui Sp. Cassium, Sp. Maelium non oderit? Cum duobus ducibus de summo imperio in Italia est decertatum, Pyrrho et Hannibale. Ab altero propter probitatem eius non minus alienis animis habemus; alterum propter crudelitatem semper haec civitas oderit.

Chi vi è che non ricordi Gaio Fabrizio e Manio Curio¹ con un certo sentimento affettuoso, pur non avendoli mai visti? Chi invece vi è che non odi Tarquinio il Superbo, non Spurio Cassio, non Spurio Melio²? Con due generali s’è combattuto in Italia per l’egemonia: Pirro e Annibale³; l’uno per la sua rettitudine non l’abbiamo in troppa avversione, l’altro per la sua crudeltà sempre questa città l’avrà in odio.

Cicerone, Laelius, de amicitia

Si riproduce il testo dell’ed. curata da R. Combes, Paris 1971 in Cicerone, L’amicizia, Milano, Rizzoli 1985 (1a), 2008 (21a) con traduzione di C. Saggio

SECONDA PARTE: tre quesiti, a risposta aperta, relativi alla comprensione e interpretazione del brano, all’analisi linguistica, stilistica ed eventualmente retorica, all’approfondimento e alla riflessione personale. Il limite massimo di estensione è di 10/12 righe di foglio protocollo. I candidati possono altresì rispondere come un scritto unitario, autonomamente organizzato nella forma del commento al testo, purché siano contenute al suo interno le risposte ai quesiti richiesti, non superando le 30/36 righe di foglio protocollo.

1) Comprensione / interpretazione

Nel testo proposto, Cicerone, per bocca di Lelio, offre argomenti per contrastare un’interpretazione utilitaristica dell’amicizia: si riporti il ragionamento, evidenziando, con motivato giudizio, le tappe che si ritengono più significative per il suo sviluppo.

2) Analisi linguistica e/o stilistica

Si individuino alcune delle soluzioni stilistiche e/o lessicali del testo che sembrano maggiormente contribuire a rendere lo spessore morale attribuito da Lelio all’amicizia, motivando le proprie scelte.

3) Approfondimento e riflessioni personali

A partire dall’antichità, la letteratura di ogni tempo immortala una nutrita galleria di personaggi legati da saldi vincoli di amicizia. Si scelgano uno o più esempi di quelli rimasti maggiormente impressi nella memoria, motivando la scelta e traendo spunto per proporre considerazioni personali sull’importanza di questo sentimento.

Liceo Scientifico

 

PROBLEMA 1

«La ragione non è nulla senza l’immaginazione» – Cartesio
Dati 𝑟 > 0 e 𝑘 < 0, si considerino la circonferenza 𝐶𝑟 , di centro l’origine e raggio 𝑟, e la funzione
𝑓𝑘 (𝑥) = 𝑘 |𝑥| .
a) Verificare che 𝑓𝑘 è continua ma non derivabile in 𝑥 = 0 qualunque sia il valore di 𝑘 .
Individuare i due valori di 𝑟 in corrispondenza dei quali 𝐶𝑟 delimita con il grafico di 𝑓𝑘 , per
opportuni valori di 𝑘 , un settore circolare nel semipiano 𝑦 ≤ 0 di area 𝜋 e contorno di
lunghezza 4 + 𝜋. Stabilito che 𝑟 = 2 è il maggiore di tali valori, in uno stesso riferimento
cartesiano 𝑂𝑥𝑦, tracciare la circonferenza 𝐶2 e il grafico della funzione 𝑓−1 .
b) Studiare la funzione 𝑔(𝑥) = √4 − 𝑥 2 , specificandone dominio, simmetrie, punti di non
derivabilità, intervalli di monotonia ed insieme immagine. Verificare che il grafico di 𝑔 coincide
con la parte di 𝐶2 che si trova nel semipiano 𝑦 ≥ 0. Spiegare perché 𝑔 non è invertibile nel
suo dominio ed esplicitare l’intervallo [𝑎; 𝑏] di ampiezza massima, con 𝑏 > 0, nel quale 𝑔
ammette una funzione inversa ℎ. Qual è l’espressione analitica di ℎ?
c) Sia 𝐴 un punto del grafico di 𝑔, situato nel I quadrante, e siano 𝑀 e 𝑅 le sue proiezioni
ortogonali sugli assi del riferimento. Determinare le coordinate di 𝐴 in modo che il quadrilatero
𝐴𝑀𝑂𝑅 abbia area massima. Dopo aver verificato che tale quadrilatero è un quadrato,
dimostrare che è anche quello di perimetro massimo.
d) Si consideri la funzione 𝐹 (𝑥) = ∫−2 √4 − 𝑡 2 𝑑𝑡, con 𝑥 ∈ [−2; 2]. Determinare 𝐹(2) e
tracciare un grafico di 𝐹 , dopo averne studiato monotonia e concavità. Scrivere, inoltre,
l’equazione della retta tangente al grafico di 𝐹 nel suo punto di flesso.

 

PROBLEMA 2
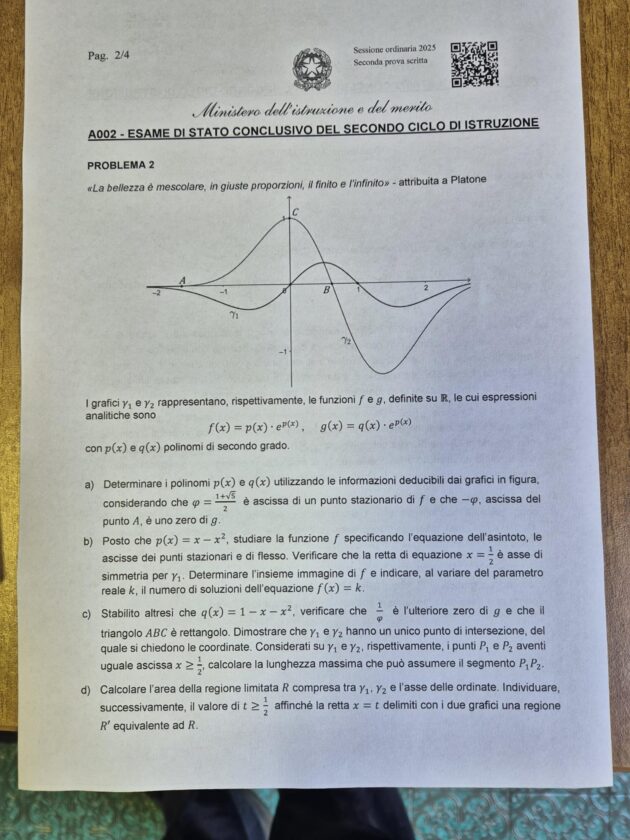
«La bellezza è mescolare, in giuste proporzioni, il finito e l’infinito» – attribuita a Platone

I grafici 𝛾1 e 𝛾2 rappresentano, rispettivamente, le funzioni 𝑓 e 𝑔, definite su ℝ, le cui espressioni
analitiche sono
𝑓 (𝑥) = 𝑝(𝑥) ∙ 𝑒 𝑝(𝑥) , 𝑔(𝑥) = 𝑞 (𝑥) ∙ 𝑒 𝑝(𝑥)
con 𝑝(𝑥) e 𝑞(𝑥) polinomi di secondo grado.
a) Determinare i polinomi 𝑝(𝑥) e 𝑞 (𝑥) utilizzando le informazioni deducibili dai grafici in figura,
considerando che 𝜑 = (1+√5)/2 è ascissa di un punto stazionario di 𝑓 e che −𝜑, ascissa del
punto 𝐴, è uno zero di 𝑔.
b) Posto che 𝑝(𝑥) = 𝑥 − 𝑥 2 , studiare la funzione 𝑓 specificando l’equazione dell’asintoto, le
ascisse dei punti stazionari e di flesso. Verificare che la retta di equazione 𝑥 = 1/2 è asse di
simmetria per 𝛾1 . Determinare l’insieme immagine di 𝑓 e indicare, al variare del parametro
reale 𝑘 , il numero di soluzioni dell’equazione 𝑓 (𝑥) = 𝑘 .
c) Stabilito altresì che 𝑞 (𝑥) = 1 − 𝑥 − 𝑥 2 , verificare che 1/𝜑 è l’ulteriore zero di 𝑔 e che il
triangolo 𝐴𝐵𝐶 è rettangolo. Dimostrare che 𝛾1 e 𝛾2 hanno un unico punto di intersezione, del
quale si chiedono le coordinate. Considerati su 𝛾1 e 𝛾2 , rispettivamente, i punti 𝑃1 e 𝑃2 aventi
uguale ascissa 𝑥 ≥ 1/2 , calcolare la lunghezza massima che può assumere il segmento 𝑃1 𝑃2 .
d) Calcolare l’area della regione limitata 𝑅 compresa tra 𝛾1 , 𝛾2 e l’asse delle ordinate. Individuare,
successivamente, il valore di 𝑡 ≥ 1/2 affinché la retta 𝑥 = 𝑡 delimiti con i due grafici una regione
𝑅′ equivalente ad 𝑅.

QUESITI

1. Dato un triangolo 𝐴𝐵𝐶 , sia 𝑀 il punto medio del lato 𝐵𝐶 e siano 𝐵′ e 𝐶′ due punti,
   rispettivamente, sul lato 𝐴𝐵 e sul lato 𝐴𝐶 , in modo tale che 𝐴𝐵′ = 1/3 𝐴𝐵 e 𝐴𝐶′ = 1/3 𝐴𝐶 .
   Dimostrare che, se i segmenti 𝑀𝐵′ e 𝑀𝐶′ sono tra loro congruenti, allora lo sono anche i lati
   𝐴𝐵 e 𝐴𝐶 .
2. Si considerino la superficie sferica di equazione (𝑥 − 1)² + (𝑦 − 2)² + 𝑧² = 1 e il piano 𝜋
   di equazione 𝑥 − 2𝑦 − 2𝑧 + 𝑑 = 0. Discutere, al variare del parametro reale 𝑑 , se il piano 𝜋
   è secante, tangente o esterno alla superficie sferica. Determinare il valore del parametro 𝑑 in
   modo che 𝜋 divida la sfera in due parti uguali.
3. L’opera futurista di Boccioni “Forme uniche della continuità nello spazio” del 1913, riportata sulla
   moneta da 20 centesimi, descrive un uomo che avanza velocemente nello spazio. Una parte del
   profilo evidenziato in figura, in un opportuno sistema di riferimento, può essere approssimato dalla
   funzione
   𝑓 (𝑥 ) = {
   −4𝑥² − 8𝑥, −1≤𝑥 ≤0
   1 + tan³(𝑥 + 𝜋/4), 0<𝑥≤2
   Tracciare il grafico di 𝑓 , dopo averne analizzato la continuità e la derivabilità nell’intervallo [−1; 2].
4. Assegnata una funzione 𝑔, derivabile in ℝ e tale che 𝑔(𝜋/4) = 𝑔′(𝜋/4) = 2, determinare
   l’equazione della retta normale alla curva 𝑦 = 𝑔(𝑥) sen²𝑥 nel suo punto di ascissa 𝜋/4.
5. Determinare il valore del parametro reale 𝑘 in modo che le due curve 𝑦 = 𝑒ˣ , 𝑦 = 6 − 𝑘𝑒⁻ˣ
   risultino tangenti tra loro, individuando le coordinate del punto di contatto.
6. Scrivere una funzione polinomiale 𝑓 in modo tale che la retta di equazione 𝑦 = 2𝑥 + 3 sia
   tangente al grafico di 𝑓 nel suo punto di ascissa 0 e si abbia ∫₀³ 𝑓(𝑥)𝑑𝑥 = 9.
7. Siccome mi sembrava che per puro caso alcuni fatti fossero avvenuti così com’erano stati
   predetti dagl’indovini, tu hai parlato a lungo del caso, e hai detto, per esempio, che si può
   ottenere il “colpo di Venere” lanciando a caso quattro dadi […].
   Cicerone, De divinatione, II, 21, 48 – traduzione e cura di S. Timpanaro, Garzanti, Milano 1999.
   Testo originale – Nam cum mihi quaedam casu viderentur sic evenire ut praedicta essent a
   divinantibus, dixisti multa de casu, ut Venerium iaci posse casu quattuor talis iactis […].
   Cicerone, nel dialogo con il fratello Quinto, parla del colpo di Venere, che consiste nel lanciare
   4 dadi a 4 facce ottenendo 4 risultati diversi. Supponendo che le facce di ciascun dado siano
   equiprobabili, determinare:
   • la probabilità di ottenere il colpo di Venere nel lancio di 4 dadi;
   • la probabilità di ottenere 4 numeri tutti uguali.
8. Quanti sono gli anagrammi, anche senza significato, della parola “STUDIARE”? In quanti di
   tali anagrammi si può leggere consecutivamente la parola “ARTE”, come ad esempio in
   “SUARTEDI”?
   Quanti sono gli anagrammi, anche senza significato, della parola “VACANZA”?

«La matematica non conosce razze o confini geografici;
per la matematica, il mondo culturale è una singola nazione»
D. Hilbert

Discipline grafiche e architettura (in gallery le pagine seguenti)

Discipline audiovisive e multimediali (in gallery le pagine seguenti)

 

CLICCA QUI PER ALTRE NOTIZIE SULLA MATURITA' 2025